The Tangle：圖解介紹

第二部：交易速率、延遲與隨機漫步

在之前的系列文章中，我們介紹了 tangle 這樣的資料結構，也了解了有關 tips 和選取好的 tip 選擇演算法的重要性。今天我們將學習有關交易速率和網路延遲，以及它們在塑造 tangle 中所扮演的角色，我們還會講解有關 無權重隨機漫步 的資訊。

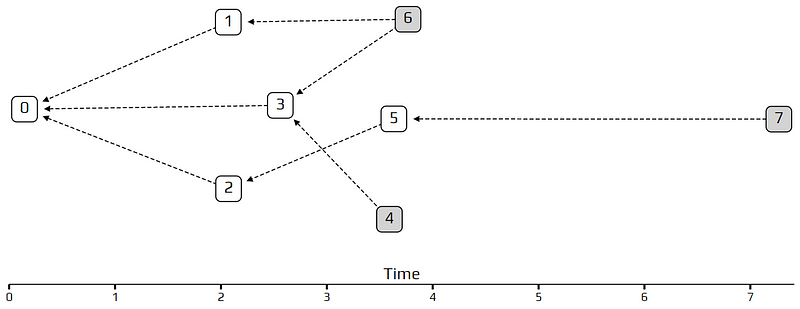
在上周的模擬你可能會發現交易並沒有按照時間平均分布，有些時段會比其他時段還要「忙碌」。這樣的隨機性是用帕松過程來組織交易抵達，這能讓模型更貼近真實情形。此模型常拿來用在分析在一段時間中有多少顧客光臨一家店面，或是有多少通電話打到客服中心。我們可以從下圖的例子中看到這樣的行為，交易 4、5、6 幾乎同時抵達，但在交易 6 之後出現了一段空窗期。

我們進行帕松過程的目的想瞭解的只有一個：交易進入的速率平均下來是個常數，而在此我們設此數為 λ。舉例來說我們設 λ=2，然後交易數量為 100，這樣整個模擬的交易時間就會大概是 50 個時間單位，你可以自己試試看！

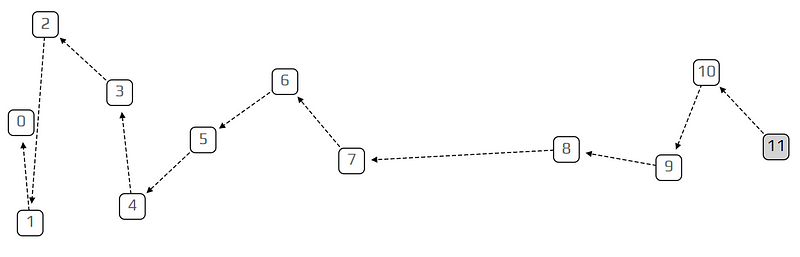
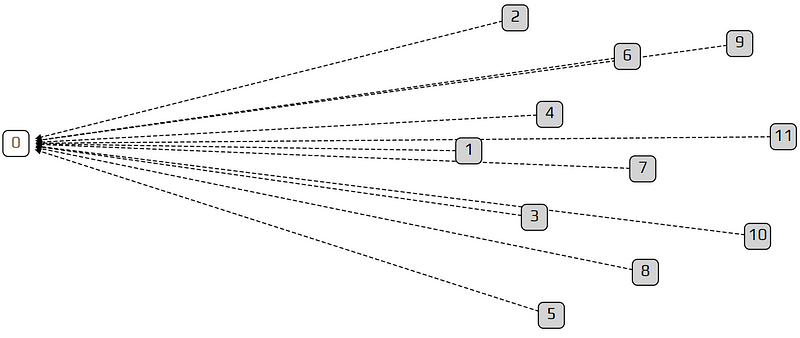
在我們繼續之前，還有一件有趣的是值得一提：如果我們設 λ 像是 0.1 這麼小的數值的話，圖形會變成一個「鏈」。一個鏈代表這個 tangle 只確認之前一項交易而已，而不是兩個。會導致這種情形是因為新加入的交易太慢，變成在任何時段都只有一個 tip 能夠確認。舉另一種極端例子的話，像是超高的 λ 反而會變成所有交易抵達超快，它們都只看見一個 tip 也就是創始交易。這只是此模擬的限制：當 λ 極高且交易數量固定時，我們只模擬了非常短暫的時間。

極低的 λ 所產生的鏈

極高的 λ 造成只有創始交易可見

所以交易看不見之前的交易指的是什麼意思呢？在模型中我們讓每筆交易剛抵達時會暫時隱藏一段時間，我們將此延遲時段用 h 來表示。這段延遲代表交易準備好在網路中傳播的時間。在我們的模擬中，我們永遠設 h=1 。這代表我們僅能確認一個時間點單位之前的交易。這樣的延遲不僅是為了更貼近現實的小細節，而更是 tangle 的基本性質，少了這樣的本質我們將永遠只會得到一串非常無聊的鏈。這也讓 tangle 更接近現實世界的狀況，每個人傳遞交易給其他人的時間總是會有延遲的。

最後是時候講解一下更進階的 tip 選擇演算法了： 無權重隨機漫步 。使用此演算法，我們設置一位 行人 在創始交易上，它會一步步「走」向 tips。每一步它會走到有直接驗證到目前所在交易的交易。我們選擇走向的交易有相等的機率，也就是我們所謂的 無權重 。我們一樣也做了個模擬顯示如何漫步的。

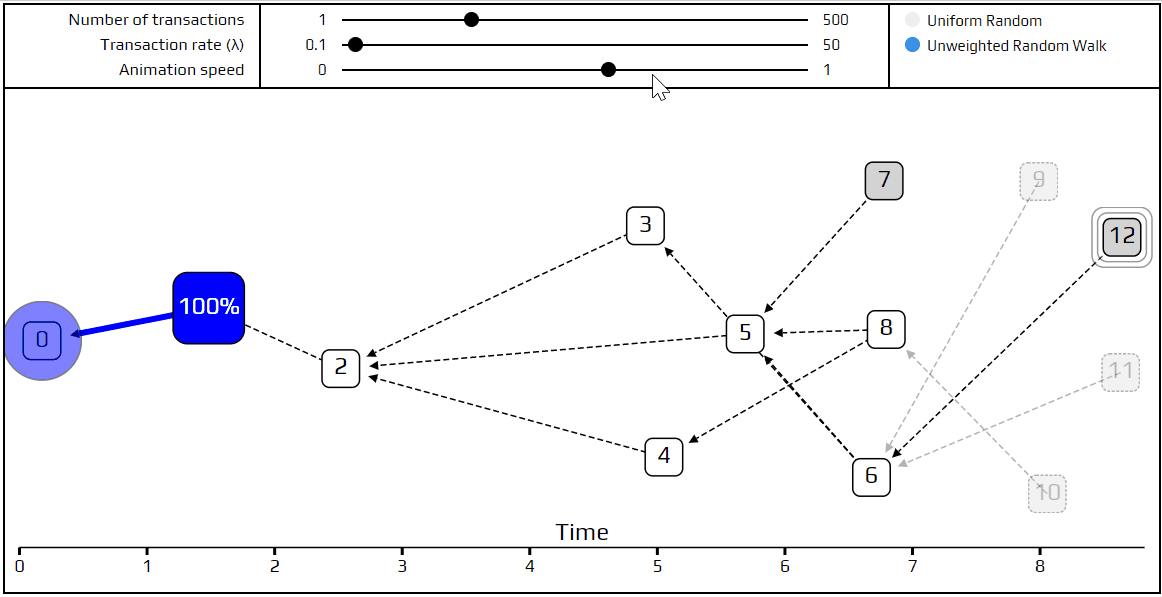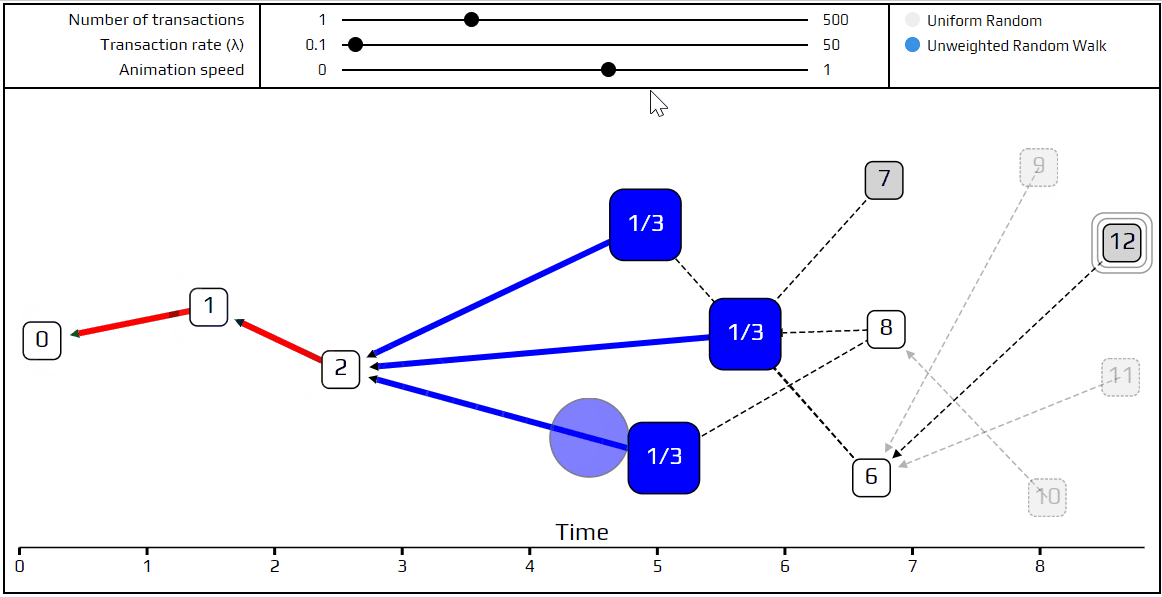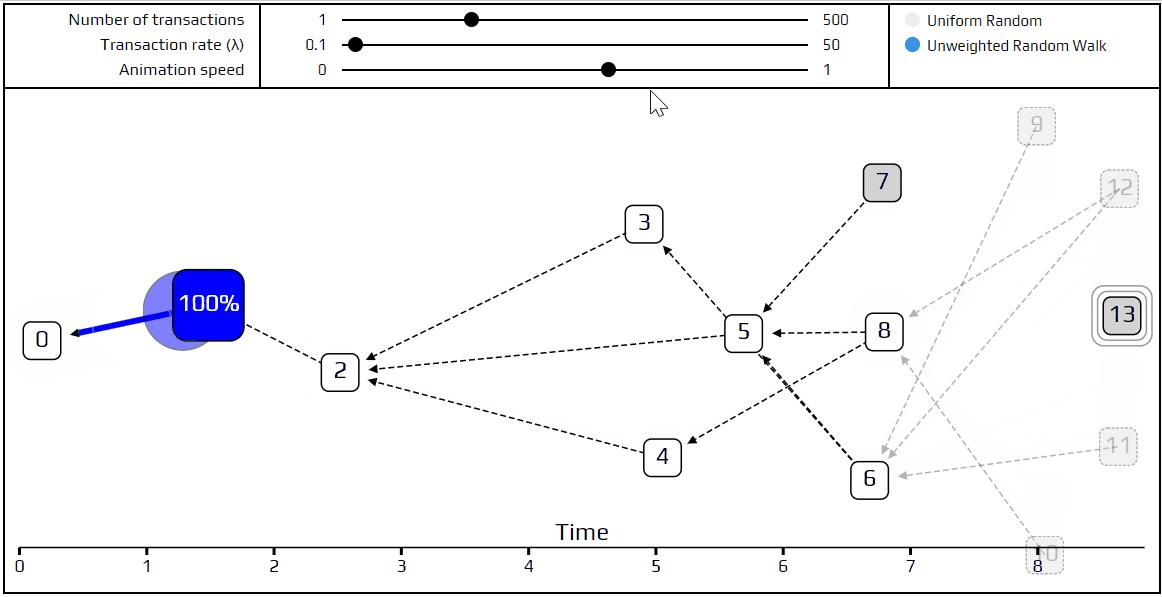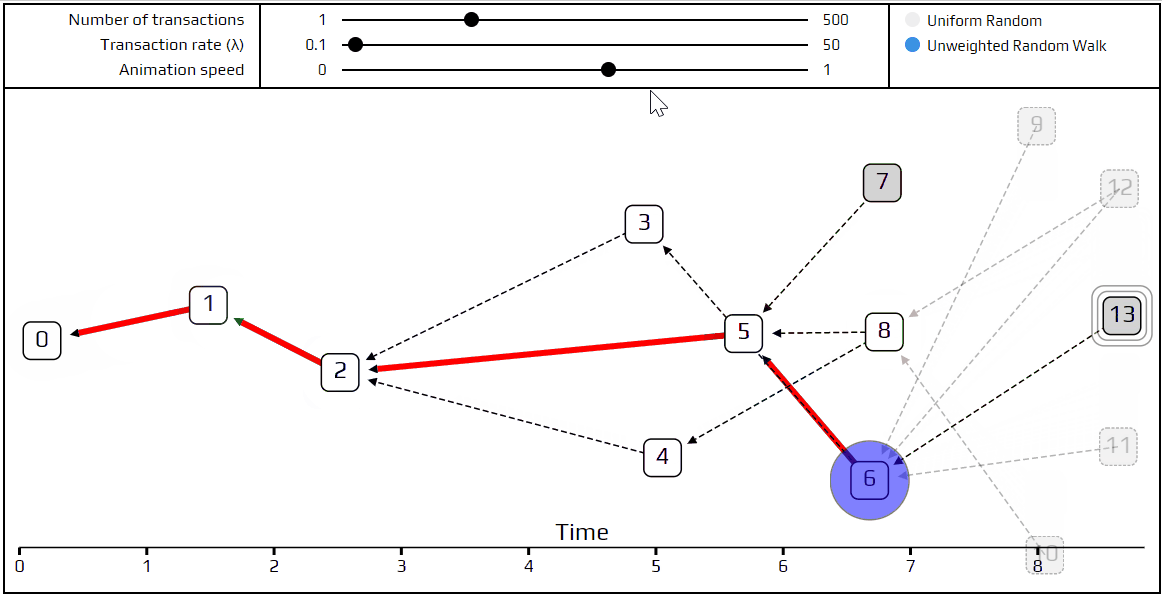
你可以看到行人行走的路徑為紅色，而下一步能行走的可能路徑標示為藍色，而最近的幾筆交易在隨機漫步中會是隱藏的，所以顯示為透明的。

今天我們介紹了不少新資訊，希望你能自己花點時間消化，玩玩看 模擬並提出問題。你可以直接在 Discord 聯絡到 @alongal#3938。下周將會討論到累積權重、馬可夫蒙地卡羅以及權重隨機漫步。